SIMULATING SOFT TISSUE WITH A TACTILE SHAPE DISPLAY
Dianne T.V. Pawluk, William J. Peine, Parris S. Wellman and Robert D. Howe
Division of Engineering and Applied Sciences
Harvard University
Cambridge, MA 02138
INTRODUCTION
One of a surgeonís most important tools is a highly developed sense of touch. Surgeons rely on sensations from the fingertips to guide manipulation and to perceive a wide variety of anatomical structures and pathologies. One important property used to assess the health of organs and tissues is compliance, which surgeons normally obtain by squeezing or indenting with their fingers.
Unfortunately, new surgical techniques, such as minimally invasive procedures and those involving robotic manipulators, separate the surgeonís hands from the surgical site. In these situations the surgeonís perception is limited to visual feedback and force feedback through the handles of long instruments. However, vision provides very little information about the compliance of an object. Furthermore, Srinivasan and LaMotte [4] have shown, in direct manipulation experiments, that kinesthetic (force-position) sensing alone is also insufficient: their subjects were unable to determine the difference between even the hardest and softest rubber samples used in the absence of the distributed skin sensation of surface deformation. This suggests that even the most accurately relayed force feedback is inadequate for compliance discrimination.
DISPLAY SYSTEM
This problem can be addressed by providing tactile, as well as kinesthetic, feedback to the surgeon. One method of conveying the needed tactile information, for both remote surgery and virtual surgical simulators, is by using a tactile display to recreate the tactile stimulus directly on the surgeonís fingertip. A tactile display is a device consisting of an array of pins which are raised and lowered to provide a sensation of surface deformation. Previously, tactile displays have primarily been considered in terms of their utility in providing small scale shape, such as during tumor localization [3].
Here, we consider what is needed to make a display feel like a compliant object. For this we must understand how the finger would have interacted with the compliant object if it was in direct contact, and then how to relay this information through a rigid shape display. The principle behind the simulated tissue interaction is that the surgeon imparts the desired contact force to the display. The stiffness display system then produces the correct deformation profile and rigid body motion, corresponding to the expected result for the real object.
The proposed tissue stiffness display system would comprise a shape display mounted on an instrumented linear actuator. The shape display is an array of closely spaced (i.e., 2 mm apart) individually actuated pins which press against the fingerpad. Shape memory alloy wires raise and lower the pins, providing the necessary tactile information [3]. The linear actuator provides the kinesthetic (force-displacement) relationship and measures the total force exerted by the surgeonís finger.
CONTACT MODEL
In order to predict the response of the fingerpad to a remote object, we need a good model of the finger-tissue interaction. Experimentally, we have begun to examine this issue by considering the dynamic contact of the human fingerpad with a flat, rigid surface [2]. We have found that the quasi-static pressure response of the fingerpad can be successfully approximated by Hertzian contact [1] modified to allow for a nonlinear variation of the modulus of elasticity. Approximating the fingerpad as a sphere, the contact pressure distribution, p(r,x), can be described by:
![]()
where r = radial distance from the center of contact,
x = maximum fingerpad deformation (i.e., at r=0),
E*f = modulus of elasticity of the fingerpad,
Rf = radius of curvature of the fingerpad, and
a(x) = radius of the contact area.
From Hertz theory, the radius of contact, a(x) is given by:
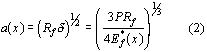
where P = total contact force, and
d = rigid body indentation.
The nonlinear varying modulus of elasticity is assumed to be given by:
![]()
where b and m are parameters of the model fit to experimental data [2].
We can generalize this model to interactions between the fingerpad and objects of varying radii and compliance by making the following substitutions in equations (1)-(2):
![]()
where Rt is the radius of curvature of the tissue, and
![]()
where Et is the modulus of elasticity and
nt is the Poissonís ratio for the tissue. Although this generalization has not been verified experimentally, it provides a preliminary estimate of the expected interaction between the fingerpad and compliant surface.
REPRODUCTION OF COMPLIANCE
To display the estimate of the objectís compliance on a shape display, we need to know the deformation profile of the fingerpad to provide the appropriate position command to each of the pins of the display. From the Hertz model, the deformation of the fingerpad, referenced to its undeformed shape F(r), is:
![]()
where
![]()
There is also an overall rigid body motion of the finger which occurs upon contact, d (in Equation 2).
To simulate tissue interaction we must measure the contact force P, which the surgeon applies to the display. We then must produce the desired motion: both the fingerpad deformation uz(r), which can be represented using the tactile shape display, and the rigid body motion d, which can be provided by the linear actuator. In order to do this, we must solve for uz(r) and d using equations (1)-(7). In these equations, the parameters describing the fingerpad, Rf, b, m, are assumed to be measured a priori, and the parameters describing the tissue, Rt, Et and nt, are assumed to be measured from the environment. Knowing the applied force P, uz(r) and d can be calculated in real-time using a Newton-Euler minimization technique.
Figure 1 shows the response of the model at an applied force of 3 N, using parameters measured for a typical fingerpad [2] in contact with a flat compliant surface (Et = 15 kPa, nt = 0.5). The solid line shows the overall fingerpad motion, whereas the dotted line shows that component (the rigid body motion) which would be provided by a kinesthetic feedback mechanism; the difference between these two is the deformation to be provided by a tactile shape display.
The maximum deflection (x = uz(0)) and rigid body motion (d) of the fingerpad contacting flat surfaces of varying compliances at force levels between 0 and 4 N are shown in Figures 2 and 3. The logarithmic effect in both responses is due to the exponentially increasing modulus of elasticity (E*f) which causes the fingerpad to become stiffer at increasing forces and therefore more difficult to deform.
REFERENCES
- Johnson, K.L. (1995). Contact Mechanics. Cambridge University Press.
- Pawluk, D.T.V. and R.D. Howe. (1996). Dynamic Contact Mechanics of the Human Fingerpad, Part II. Harvard Robotics Lab Tech. Report 96-004.
- Peine, W.J., D.A. Kontarinis and R.D. Howe. (1995). A Tactile Sensing and Display System for Surgical Applications. In Satava, R.M. et al. (eds.) Interactive Technology and the New Paradigm for Healthcare,Washington.
- Srinivasan, M.A. and R.H. LaMotte (1995). Tactual Discrimination of Softness. J. Neurophys. 73 (1).
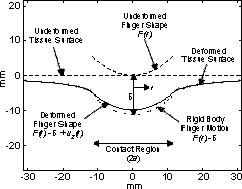
Figure 1.
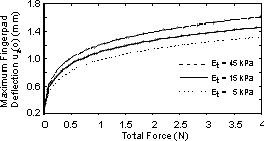
Figure 2.
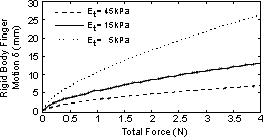
Figure 3.